Sequential Quadratic Programming (SQP)
A gradient-based iterative optimization method and is considered to be the best method for nonlinear problems by some theoreticians. In HyperStudy, Sequential Quadratic Programming has been further developed to suit engineering problems.
Usability Characteristics
- A gradient-based method, therefore it will most likely find the local optima.
- One iteration of Sequential Quadratic Programming will require a number of simulations. The number of simulations required is a function of the number of input variables since finite difference method is used for gradient evaluation. As a result, it may be an expensive method for applications with a large number of input variables.
- Sequential Quadratic Programming terminates if one of the conditions below are
met:
- One of the two convergence criteria is satisfied.
- Termination Criteria is based on the Karush-Kuhn-Tucker Conditions.
- Input variable convergence
- The maximum number of allowable iterations (Maximum Iterations) is reached.
- An analysis fails and the Terminate optimization option is the default (On Failed Evaluation).
- One of the two convergence criteria is satisfied.
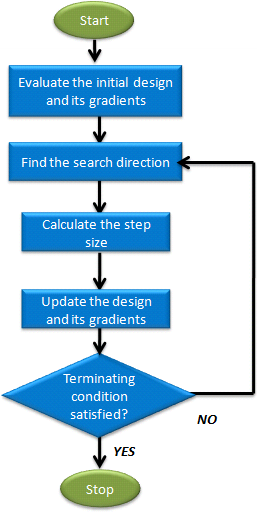
Figure 1. Sequential Quadratic Programming Process Phases
Settings
| Parameter | Default | Range | Description |
|---|---|---|---|
| Maximum Iterations | 25 | > 0 | Maximum number of iterations allowed. |
| Constraint Violation Tol. (%) | 0.1 | > 0.0 | Global maximum allowable percentage constraint violation. Constraints must not be violated by more than this value in the converged design. |
| Design Variable Convergence | 0.0 | >=0.0 |
Input variable convergence parameter. Design has converged when
there are two consecutive designs for which the change in each input
variable is less than both (1) Design Variable
Convergence times the difference between its bounds, and (2)
Design Variable
Convergence times the absolute value of its initial value
(simply Design
Variable Convergence if its initial value is zero). There also
must not be any constraint whose allowable violation is exceeded in the
last design.
Note: A larger value allows for faster convergence, but
worse results could be achieved.
|
| On Failed Evaluation | Terminate optimization |
|
|
| Parameter | Default | Range | Description |
|---|---|---|---|
| Termination Criteria | 1.0e-4 | >0.0 | Defines the termination criterion, relates to satisfaction of
Kuhn-Tucker condition of optimality. Recommended range: 1.0E-3 to 1.0E-10. In general, smaller values result in higher solution precision, but more computational effort is needed. For the nonlinear optimization problem:
Sequential Quadratic Programming is
converged if:
|
| Sensitivity | Forward FD |
|
Defines the way the
derivatives of output responses with respect to input variables are
calculated.
Tip: For higher solution precision, 2 or 3 can be used,
but more computational effort is consumed.
|
| Max Failed Evaluations | 20,000 | >=0 | When On Failed Evaluations is set to Ignore failed evaluations (1), the optimizer will tolerate failures until this threshold for Max Failed Evaluations. This option is intended to allow the optimizer to stop after an excessive amount of failures. |
| Constraint Threshold | 1.0e-4 | > 0.0 |
Used for constraint value
calculation. In general, constraint value is normalized to its bound
value. One exception is that, constraint value is not normalized if its
absolute bound value is less than this parameter.
Tip: Recommended range is 1.0e-6 ~ 1.0.
|
| Use Perturbation size | No | No or Yes | Enables the use of Perturbation Size, otherwise an internal automatic perturbation size is set. |
| Perturbation Size | 0.0001 | > 0.0 |
Defines the size of the finite difference perturbation. For a variable x, with upper
and lower bounds (xu and xl, respectively), the following logic is used
to preserve reasonable perturbation sizes across a range of variables
magnitudes:
|
| Use Inclusion Matrix | No |
|
|