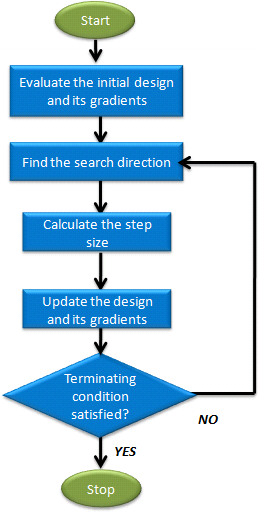
Method of Feasible Directions (MFD)

Used for solving constrained optimization problems.

Usability Characteristics

A gradient-based method, which will most likely find the local optima.
May be efficient with a large number of constraints, but in general it is less accurate than Sequential Quadratic Programming and less efficient than Adaptive Response Surface Method.
One iteration of Method of Feasible Directions will require a number of simulations. The number of simulations required is a function of the number of input variables since finite difference method is used for gradient evaluation. As a result, it may be an expensive method for applications with a large number of input variables.
Method of Feasible Directions terminates if one of the conditions below are met:
- One of the two convergence criterias are satisfied.
  - Absolute convergence (Absolute Convergence)
  - Relative convergence (Relative Convergence (%))
- The maximum number of allowable iterations (Number of Evaluations) is reached.
- An analysis fails and the “Terminate optimization” option is the default (On Failed Evaluation).

Settings

In the Specifications step, change method settings from the Settings and More tabs.

Note: For most applications the default settings work optimally, and you may only need to change the Maximum Iterations and On Failed Evaluation.

Table 1. Settings Tab
Parameter	Default	Range	Description
Maximum Iterations	25	>0	Maximum number of iterations allowed.
Absolute Convergence	0.001	>0.0	Determines an absolute convergence tolerance, which is constant and equal to Absolute Convergence, times the initial objective function value. The design has converged when there are three consecutive designs for which the absolute change in the objective function is less than this tolerance. There also must not be any constraint whose allowable violation is exceeded in these three consecutive designs. Note: A larger value allows for faster convergence, but worse results could be achieved. ${\begin{matrix} c_{\max}^{i} \leq g_{\max} \\ \| f^{i} - f^{i - 1} \| < ε \\ i = k, k - 1, k - 2 \end{matrix}$ where $f$ is the objective value; $k$ is the current iteration number; $ε$ is the absolute convergence parameter; $c_{\max}$ is the maximum constraint violation; $g_{\max}$ is the allowable constraint violation.
Relative Convergence (%)	1.0	>0.0	The design has converged if the relative (percent) change in the objective function is less than this value for three consecutive designs. There also must not be any constraint whose allowable violation is exceeded in these three consecutive designs. Note: A larger value allows for faster convergence, but worse results could be achieved. ${\begin{matrix} c_{\max}^{i} \leq g_{\max} \\ {\begin{matrix} \| \frac{f^{i} - f^{i - 1}}{f^{i - 1}} \| < ε, if(\| f^{i - 1} \| {>10}^{- 10}) \\ \| f^{i} - f^{i - 1} \| < ε, if(\| f^{i - 1} \| \leq 10^{- 10}) \end{matrix} \\ i = k, k - 1, k - 2 \end{matrix}$ where $f$ is the objective value; $k$ is the current iteration number; $ε$ is the relative convergence parameter, $c_{\max}$ is the maximum constraint violation; $g_{\max}$ is the allowable constraint violation.
Constraint Violation Tol. (%)	0.5	>0.0	Global maximum allowable percentage constraint violation. Constraints must not be violated by more than this value in the converged design.
On Failed Evaluation	Terminate optimization	Terminate optimization (default) Ignore failed evaluations	Terminate optimization Terminates with an error message when an analysis run fails. Ignore failed evaluations Ignores the failed analysis run, and tries different step sizes to do line search.

Table 2. More Tab
Parameter	Default	Range	Description
Max Failed Evaluations	20,000	>=0	When On Failed Evaluations is set to Ignore failed evaluations (1), the optimizer will tolerate failures until this threshold for Max Failed Evaluations. This option is intended to allow the optimizer to stop after an excessive amount of failures.
Constraint Threshold	1.0e-4	>0.0	Used for constraint value calculation. In general, constraint value is normalized to its bound value. One exception is that, constraint value is not normalized if its absolute bound value is less than this parameter. Tip: Recommended range is 1.0e-6 ~ 1.0.
Use Perturbation size	No	No or Yes	Enables the use of Perturbation Size, otherwise an internal automatic perturbation size is set.
Perturbation Size	0.0001	>0.0	Defines the size of the finite difference perturbation. For a variable x, with upper and lower bounds (xu and xl, respectively), the following logic is used to preserve reasonable perturbation sizes across a range of variables magnitudes: If abs( x) >= 1.0 then perturbation = Perturbation Size * abs( x) If (xu - xl) < 1.0 then perturbation = Perturbation Size * (xu – xl) Otherwise perturbation = Perturbation Size
Use Inclusion Matrix	No	No With Initial Without Initial	No Ignores the Inclusion matrix With Initial Runs the initial point. The best point of the inclusion or the initial point is used as the starting point. Without Initial Does not run the initial point. The best point of the inclusion is used as the starting point.