Linear and Nonlinear Analysis

However, the implicit algorithm uses a global resolution which requires convergence for each time step and has low robustness in comparison to the explicit (null pivots, divergence for high nonlinearities, etc.).

The implicit methods result in solving a linear system for each time step, which is relatively expensive but enables a large time step: few expensive calculations. The explicit method treats linear or nonlinear systems depending on the problem. It is less expensive and faster for each step, but requires short time steps to ensure stability of the scheme that has many inexpensive cycles.
Newmark β
Implicit integration scheme

This scheme is unconditionally stable, the stability condition being independent of the time step choice. See the Radioss Theory Manual for further information about the Newmark scheme.

Radioss has a linear and a nonlinear solver. Only static computations are available and loading should be defined as a monotonous increasing time function for nonlinear analysis.

The main computational methods available in Radioss:
  • Cholesky (direct method, linear solver)
  • Preconditioned Conjugate Gradient (linear solver)
  • Modified Newton-Raphson method (nonlinear solver)
The precondition methods for linear solver available in Radioss:
  • No preconditioned
  • Diagonal Jacobi
  • Incomplete Cholesky
  • Stabilized incomplete Cholesky
  • Factored Approximate Inverse (by default)

You should define the tolerance and stop criterion for the linear and nonlinear solver (residual).

Strategies of resolution for nonlinear static computation/time step control:
  • Iterations number limit for updating stiffness matrix
  • Convergence iterations number for increasing time step
  • Convergence iterations number for decreasing time step
  • Increase time step factor
  • Decrease time step factor
  • Minimum time step
  • Maximum time step
  • Initial time step
The nonlinear solver uses the modified Newton-Raphson method and the resolution is based on sparse iterative techniques

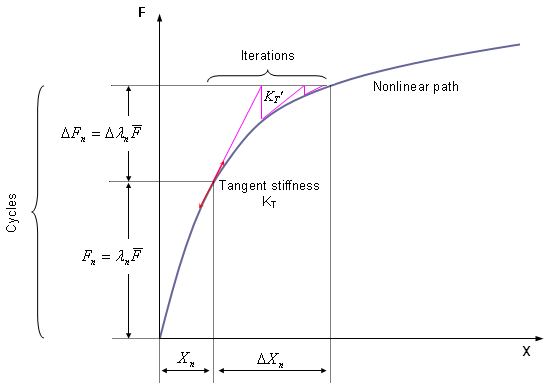
rad_ex_fig_16-19
Figure 1. Newton-Raphson Resolution in the Case of Load Control Technique
.

The modified Newton-Raphson method is based on maintaining the tangent matrix for all iterations and can be combined with the line search acceleration technique for accelerating convergence.

Piloting techniques available in Radioss:
  • Displacement norm control
  • Arc-length control

An automatic time step control is used.

Static Analysis and Implicit Options

This example deals with two implicit analysis':
  • A static linear computation (loading by gravity),
  • A static nonlinear computation (three computations are performed: dummy positioning using an imposed displacement, followed by a concentrated load and a gravity loading).

An adapted modeling methodology is set up for each analysis. Contact with the different interfaces depends on the computations taken into account and then the material can be updated.

The goal for this analysis is to propose a modeling method for different loading cases, with specific input data used in the implicit strategies. The studies by linear implicit and nonlinear implicit using imposed displacement are no longer comparable with results obtained by explicit due to the different physical approaches. Comparisons are only valid for the positioning by gravity loading.