Gse

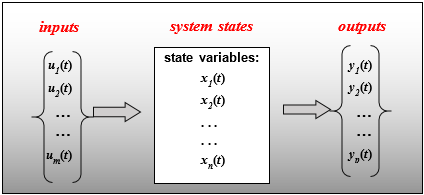
Model ElementGse is an abstract modeling element that defines a generic dynamic system. The dynamic system is characterized by a vector of inputs u, a vector of dynamic states x, and a vector of outputs y. The state vector x is defined through a set of differential equations.

Class Name

Gse

Description

The output vector y is defined by a set of algebraic equations. The image below illustrates the concept of a dynamic system.


Figure 1.

Attribute Summary

Name Property Modifiable by command? Designable?
id Int ()   NO
label Str () ✓
no Int ()  
ns Int ()  
x Reference ("Array") ✓
y Reference ("Array") ✓
u Reference ("Array") ✓
ic Reference ("Array") ✓
static_hold Bool () ✓
implicit Bool ()  
function Function ("GESSUB") ✓
routine Function ()  
active Bool () ✓

Usage

# Defined in a compiled user-written subroutine
Gse (no=int, function=userString, routine=string optional_attributes)

# Defined in a Python function
Gse (no=int, function=userString, routine=functionPointer optional_attributes)

Attributes

Defined in a compiled user-written subroutine
no
Integer
An integer that specifies the number of outputs in the GSE.
no > 0
This attribute is mandatory.
function
String
Specifies the list of parameters that are passed from the data file to the user-defined subroutines GSESUB, GSEXX, GSEXU, GSEYX and GSEYU. You must write GSESUB. The others, GSEXX, GSEXU, GSEYX and GSEYU, are optional. When these are not written, MotionSolve will generate the partial derivatives automatically via finite differencing.
The function attribute is mandatory.
routine
String
Specifies an alternative name for the user subroutine. The name consists of two pieces of information, separated by "::". The first is the pathname to the shared library containing the function that computes the response of the user-defined Variable. The second is the name of the function in the shared library that does the computation. An example is: routine="/staff/Altair/engine.dll::myGse"
  • "/staff/Altair/ engine.dll is the dll
  • "myGse" is the function within this DLL that performs the calculations
The attribute routine is optional. When not specified, routine defaults to GSESUB.
Defined in a Python function
no
Integer
An integer that specifies the number of outputs in the GSE.
no > 0
This attribute is mandatory.
function
String
Specifies the list of parameters that are passed from the data file to the user-defined subroutines GSESUB, GSEXX, GSEXU, GSEYX and GSEYU. You must write GSESUB. The others, GSEXX, GSEXU, GSEYX and GSEYU, are optional. When these are not written, MotionSolve will generate the partial derivatives automatically via finite differencing.
The function attribute is mandatory.
routine
Pointer to a callable function in Python
An example is: routine=myGse
  • myGse is a Python function or method that can be called from wherever the model resides.
The attribute routine is optional. When not specified it defaults to GSESUB.routine
Optional attributes - available to all variants
id
Integer
Specifies the element identification number. This number must be unique among all the GSE objects in the model.
This attribute is optional. MotionSolve will automatically create an ID when one is not specified.
Range of values: id > 0
label
String
Specifies the name of the GCON object.
This attribute is optional. When not specified, MotionSolve will create a label for you.
u
Reference to an Array object of type U.
Specifies the ARRAY used to store the input u of this GSE. You can use the ARYVAL() function with this ID to access the states in a MotionSolve expression. You can also use this ID in SYSFNC and SYSARY to access the input values from a user subroutine.
This attribute is optional.
y
Reference to an Array object of type Y.
Specifies the ARRAY used to store the output, y, of this GSE. You can use the ARYVAL() function with the ID of this array to access the states in a MotionSolve expression. You can also use this ID in SYSFNC and SYSARY to access the output values from a user subroutine.
This attribute is optional.
x
Reference to an Array object of type X,
Specifies the ARRAY used to store the states x of this GSE. You can use the ARYVAL() function with the ID of this Array to access the states in a MotionSolve expression. You can also use this ID in SYSFNC and SYSARY to access the state values from a user subroutine.
This attribute is mandatory.
ic
Specifies the Array used to store the initial values of the states, x of this GSE. You can use the ARYVAL() function with the id of this Array to access the states in a MotionSolve expression. You can also use this ID in SYSFNC and SYSARY to access the initial state values from a user subroutine.
static_hold
Boolean
Specifies whether the value of the dynamic state is kept fixed or not during static equilibrium and quasi static solutions.
  • True implies that the value of the dynamic state is kept constant during static and quasi-static solutions.
  • False implies that the value of the dynamic state is allowed to change during static equilibrium or quasi-static solutions.
This attribute is optional. When not specified it defaults to False.
implicit
Boolean
A Boolean that specifies whether the differential equations defining the states are implicit or explicit.
  • True implies that the differential equations are implicitly and the equations define the residue of the differential equations.
  • False implies that the differential equations are explicitly defined and the equations define the time derivative of the states.
This attribute is optional. When not specified, implicit defaults to False.
active
Bool
Select one from True or False.
  • True indicates that the element is active in the model and it affects the behavior of the system
  • False indicates that the element is inactive in the model and it does not affect the behavior of the system. It is almost as if the entity was removed from the model, of course with the exception that can be turned "ON" when desirable.
The attribute active is optional. When not specified, active defaults to True

Example

  1. Use a GSE to define the LuGre model of friction.
    ################################################################################
# Model definition                                                             #
################################################################################
def
 sliding_block (out_name):
  m       = Model (output=out_name)

  # Model units, Gravity and Integrator settings
  units   = Units    (mass="KILOGRAM", length="METER", time="SECOND", force="NEWTON")
  grav    = Accgrav  (jgrav=-9.800)
  gstiff  = Integrator (error=1e-5)
  # Points and Vectors that will be reused
  p0      = Point (10,0,0)
  ux      = Vector (1,0,0)
  uy      = Vector (0,1,0)
  uz      = Vector (0,0,1)
  
  # Ground part and global coordinate system
  grnd    = Part (ground=True)
  oxyz    = Marker (body=grnd, label="Global CS")
  
  # Block
  blk     = Part (mass=1, ip=[4.9e-4,4.9e-4,4.9e-4], label="Block")
  blk.cm  = Marker (body=blk, qp=p0, zp=p0+uz, xp=p0+ux, label="Block CM")
  
  # Translational joint between Block and Ground along global X-axis
  im      = Marker (body=blk,  qp=p0, zp=p0+ux, xp=p0+uz, label="Joint Marker on Ground")
  jm      = Marker (body=grnd, qp=p0, zp=p0+ux, xp=p0+uz, label="Joint Marker on Ground")
  jnt     = Joint (type="TRANSLATIONAL", i = im, j = jm, label="Trans Joint")
  
  # An external force trying to move the block
  sfojm   = Marker (body=grnd, qp=p0, zp=p0+ux, xp=p0+uz, label="Sforce reaction")
  sf      = Sforce (type="TRANSLATION", actiononly=True, i=im, j=sfojm, label="Actuation Force", function = "3*sin(2*pi*time)")  

# Friction in the joint
  m.lugre = LuGre(joint=jnt)
  
  # Some requests of interest
  m.r1    = Request (type="DISPLACEMENT", i=im, j=jm, rm=jm, comment="Joint displacement")
  m.r2    = Request (type="FORCE",        i=im, j=jm, rm=jm, comment="Joint forces")
  m.r3    = Request (type="VELOCITY",     i=im, j=jm, rm=jm, comment="Joint velocity")
  
  so      = Output (reqsave=True)
  
  # Return the model you just defined
  return m

###############################################################################
###############################################################################
###############################################################################

m = sliding_block("lugre1")
m.simulate (type="DYNAMICS", end=4, dtout=.01)

# Change the static friction coefficient and continue simulation
m.lugre.mus=0.5  
m.simulate (type="DYNAMICS", end=8, dtout=.01)

Comments

  1. See Properties for an explanation about what properties are, why they are used, and how you can extend these.
  2. For a more detailed explanation about Gse, see Control: StateEqn