Fractional Factorial
A factorial experiment in which only a chosen fraction of the combinations required for the Full Factorial DOE is run.
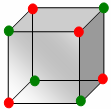
Figure 1. . The green dots illustrate the combinations a Fractional Factorial design considers.
This reduction in computational effort comes at the cost of an inability to completely resolve all of the main effects and interactions. Higher order interactions are often confounded with each other and, in some cases, can be confounded with the two-factor interactions. For example, for factors A, B, and C, each at two levels, only four runs would be required to resolve the main effects. However, all of the two-factor interactions would be confounded with the main effects (A:BC, B:AC, C:AB).
When applicable, the orthogonal arrays from other schemes, such as Plackett Burman or Taguchi, are used internally to reduce run count.
- Resolution III
- The effects are resolved with respect to each other, but all of the effects are confounded with the two-factor interactions.
- Resolution IV
- The effects are resolved with respect to each other and the two-factor interactions, but the two-factor interactions are confounded with respect to each other.
- Resolution V
- The effects are resolved with respect to each other and the two-factor interactions, and the two-factor interactions are resolved with respect to each other.
Usability Characteristics
- The desired resolution will determine the number of runs in the DOE.
- Resolution type III should only be used when on applications in which the interactions are known to be small with respect to the effects. This makes the confounding unimportant.
- When all variables have only two levels and the resolution is type III, avoiding the confounding between the effects and specified two-factor interactions can be achieved by using the Interactions tab.
- The techniques used to generate the run matrix work most effectively when variables have the same number of levels.
- Any data in the inclusion matrix is combined with the run data for post-processing. Any run matrix point which is already part of the inclusion data will not be rerun.
- Having consistent levels across the input variables makes Fractional Factorial more efficient.
Settings
| Parameter | Default | Range | Description |
|---|---|---|---|
| Resolution | III | III, IV, V | Select the resolution. |
| Number of Runs | Dependent upon the selected resolution | Any positive integer | Number of new designs to be evaluated. |
| Use Inclusion Matrix | Off | Off or On | Concatenation without duplication between the inclusion and the generated run matrix. |