OS-T: 1371 Brake Squeal Analysis of Brake Assembly
In this tutorial you will perform a brake squeal analysis on a brake assembly. Disc brakes are operated by applying a clamping load using a set of brake pads on the disc. The friction generated between the pads and the disc causes deceleration, and can potentially induce a dynamic instability of the system. This phenomena is known as brake squeal.
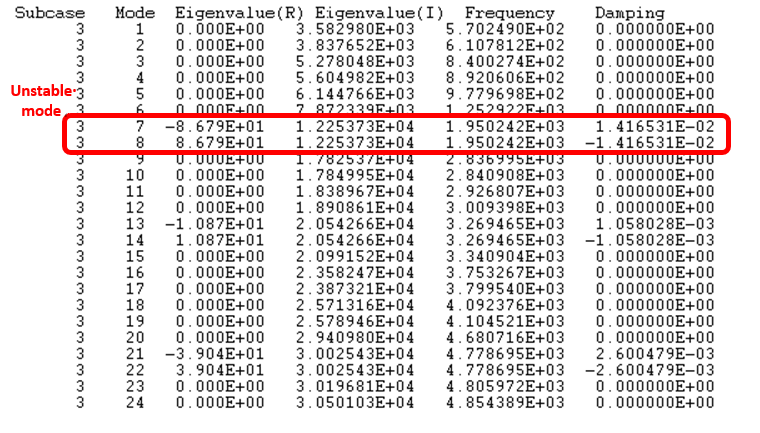
For this model OptiStruct will predict an unstable mode and the instability is seen to occur at the point of mode coalescence, i.e., a pair of modes occur at the same frequency (mode coupling), and one of them is unstable. The unstable mode can be identified during complex eigenvalue extraction because the real part of the eigenvalue corresponding to an unstable mode is positive.
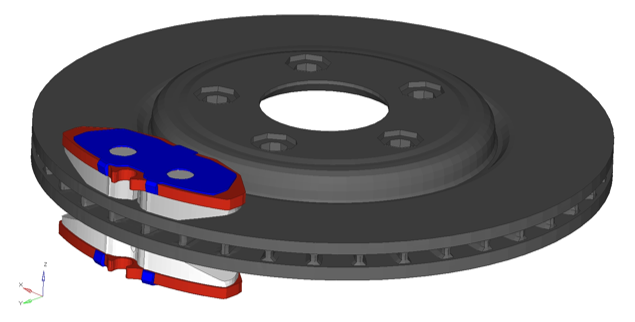
Figure 1. Model Review
brsq.fem File Data
- Hexahedral Mesh is created for the brake assembly
- All parts are defined with material MAT1
- All parts are defined with Solid Element Property
- A cylindrical coordinate system is defined with respect to the disc
- S2S Contacts are defined between brake pad and disc
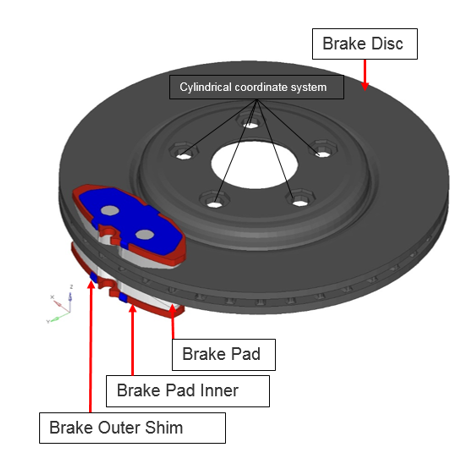
Figure 2.
- Sub-case CLAMPLOAD: Nonlinear static analysisPressure Load on Insulator (Inner and Outer), with SPC (DOF1).
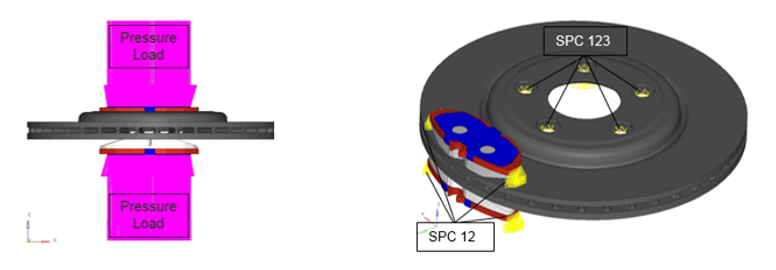
Figure 3. - Sub-case ROTOR: Nonlinear static analysis with CNTNLSUB.
Pressure Load on Pad and Rotation of the Disc, with non-zero SPC (DOF2).
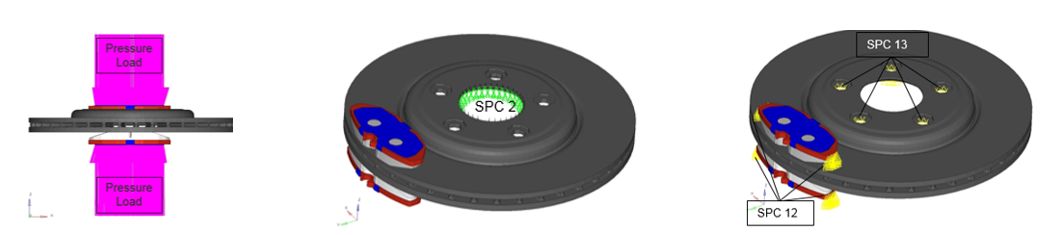
Figure 4.Tip:- The prescribed rotation should be large enough to ensure the contact between the disc and the pad is in kinetic friction, but small enough to ensure small displacement NLSTAT.
- Kinetic friction is a constant value (independent of velocity), hence prescribing rotation using SPCD is equivalent to prescribing rotational speed. The important outcome is that the contact nodes are in kinetic friction mode and it does not matter how fast or how far you move this using SPCD.
Launching HyperMesh and Setting the OptiStruct User Profile
Importing the Model
Setting Up the Model
Creating EIGRL and EIGC Cards
Defining Load Step for Modal Complex Eigenvalue Analysis
Submitting the Job
Viewing the Results
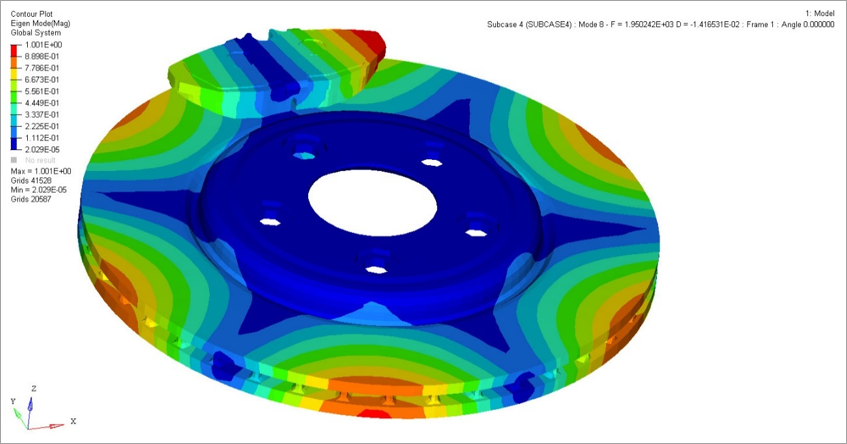
brsq.out file. The complex
eigenvectors can be reviewed in HyperView. .
.