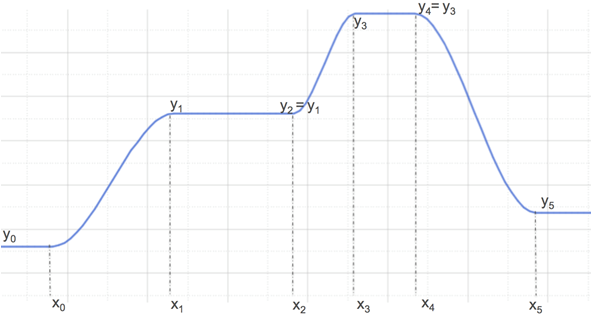
mstep
For a given set of x values, returns a vector of values that smoothly transitions from (or steps from) one level of y value to another. This function can create a vector that has many steps and can use different forms of interpolating step functions.
Syntax
mstep(x_vector, use_abs_steps, interp_key, x0, y0, x1, y1, [x2,x3,y3], [x4,x5,y5]…[xn-1,xn,yn])
Argument
- x_vector
- The independent vector x.
- use_abs_steps
- Indicates whether the y values should be considered as absolute values or relative to the previous step value. Valid values are 0 and 1. A value of 0 will consider a relative step while 1 will consider absolute values.
- interp_key
- Indicates the type of function to be used for interpolation. See Comments below.
- x0, x1, x2,..xn-1, xn
- Values of x at which the step changes.
- y0, y1, y2,..yn
- Values of y from or to which the step needs to be taken.
Example 1
Single step with absolute values and uses the step interpolation.
x = 0:100:1
y = mstep(x,1,1,20,10,40,20)
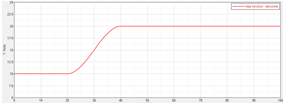
Example 2
Single step with relative values and uses the step5 interpolation.
x = 0:100:1
y = mstep(x,0,2,20,10,40,20)
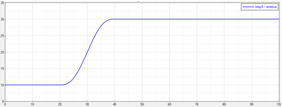
Example 3
Multiple step with relative values and uses the havsin interpolation.
x = 0:100:1
y = mstep(x,0,1,20,10,40,20,50,70,35,80,90,-50)
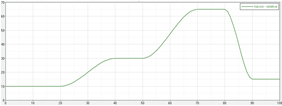
Comments
This function can be used to generate curve with multiple steps and is generally used during post processing of MotionSolve results or be used in MotionView
This function can use any of the following interpolations through different interp_key.
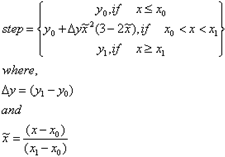
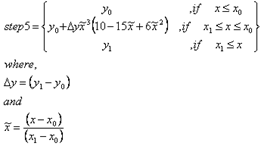
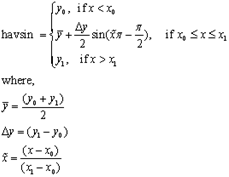
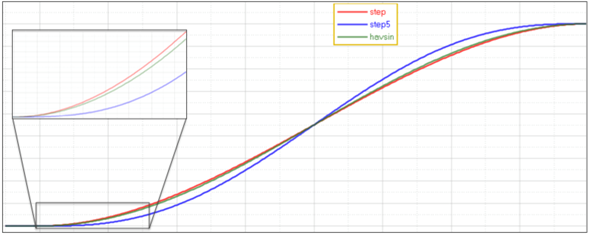
This function needs a minimum of seven arguments to generate one step. Subsequently, more steps can be created with additional arguments in sets of 3, such as 10, 13, 16 arguments and so on. The additional three arguments are 1) x at which the next step begins, 2) x at which the step ends and 3) y to which step ends. Note that the y at which step begins is already known from the previous y value. For example, mstep(x,1,1,x0,y0,x1,y1,x2,x3,y3,x4,x5,y5) is demonstrated below.