EMISSIVITY_MODEL

Specifies an emissivity model for the radiation equation.

Type

AcuSolve Command

Syntax

EMISSIVITY_MODEL("name") {parameters...}

Qualifier

User-given name.

Parameters

type (enumerated) [=constant]

Type of the emissivity.

constant or const: Constant emissivity. Requires emissivity.
piecewise_linear or linear: Piecewise linear curve fit. Requires curve_fit_values and curve_fit_variable.
cubic_spline or spline: Cubic spline curve fit. Requires curve_fit_values and curve_fit_variable.
user_function or user: User-defined function. Requires user_function, user_values and user_strings.

emissivity or emis (real) >0 <=1 [=1]

Constant value of the emissivity. Used with constant type.

diffused_fraction (real) [= 1.0]

To enable specular reflection a RADIATION_SURFACE must be defined and the diffused fraction,

a

, and emissivity,

ε

, must both be less than one.

curve_fit_values or curve_values (array) [={0,0}]

A two-column array of independent-variable/emissivity data values. Used with piecewise_linear and cubic_spline types.

curve_fit_variable or curve_var (enumerated) [=temperature]

Independent variable of the curve fit. Used with piecewise_linear and cubic_spline types.

temperature or temp: Temperature.

user_function or user (string) [no default]

Name of the user-defined function. Used with user_function type.

user_values (array) [={}]

Array of values to be passed to the user-defined function. Used with user_function type.

user_strings (list) [={}]

Array of strings to be passed to the user-defined function. Used with user_function type.

multiplier_function (string) [=none]

User-given name of the multiplier function for scaling the viscosity. If none, no scaling is performed.

Description

This command specifies an ideal grey-surface emissivity model for the radiation equation. This model is only applicable to radiation surfaces, and is not used for the radiation_heat_flux variable in the ELEMENT_BOUNDARY_CONDITION command.

EMISSIVITY_MODEL commands are referenced by RADIATION_SURFACE commands:

EMISSIVITY_MODEL( "my emissivity model" ) {
   type                                = constant 
   emissivity                          = 0.5
}
RADIATION_SURFACE( "hot wall" ) {
	emmissivity_mdoel               = "my emmissivity model"
	...
}

The emissivity is the factor

ε

in the Stefan-Boltzmann law for the total emissive power of an ideal grey surface:(1)

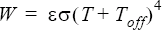
where $σ$ is the Stefan-Boltzmann constant, given by the Stefan_boltzmann_constant parameter of the RADIATION command; T is the temperature; and T_off is the offset to convert to an absolute temperature, given by the absolute_temperature_offset parameter of the EQUATION command.

A constant emissivity model applies a spatially constant emissivity, as in the above example.

Emissivity models of types piecewise_linear and cubic_spline may be used to define emissivity as a function of a single independent variable. For example,

EMISSIVITY_MODEL( "curve fit emissivity model" ) {
   type               = piecewise_linear
   curve_fit_values   = { 273, 0.2 ; 323, 0.2 ;    373, 0.3 ;    423, 0.4 ; }
   curve_fit_variable = temperature
}

defines emissivity as a function of temperature. In general, the problem must contain the variable defined by curve_fit_variable; this is not an issue here since radiation problems always contain temperature. The curve_fit_values parameter is a two-column array corresponding to the independent variable and the emissivity values. The independent variable values must be in ascending order. The limit point values of the curve fit are used when curve_fit_variable falls outside of the curve fit limits.

The curve_fit_values data may be read from a file. For the above example, the curve fit values may be placed in a file, such as emissivity.fit:

273      0.2
323      0.2
373      0.3
423      0.3

and read by:

EMISSIVITY_MODEL( "curve fit emissivity model" ) {
   type               = piecewise_linear
   curve_fit_values   = Read( "emissivity.fit" )
   curve_fit_variable = temperature 
}

An emissivity of type user_function may be used to model more complex behaviors; see the AcuSolve User- Defined Functions Manual for a detailed description of user-defined functions.

For example, consider an emissivity that is equal to 0.5 between temperatures of 300 and 400, and 0.3 otherwise. The input command may be given by:

EMISSIVITY_MODEL( "UDF emissivity model" ) {
   type          = user_function 
   user_function = "usrEmissivityExample"
   user_values   = { 300,    # lower temp. limit of band    
                     400,    # upper temp. limit of band    
                       0.3,  # default emissivity    
                       0.5 }   # emissivity in temperature band
}

where the user-defined function "usrEmissivityExample" may be implemented as follows:

#include "acusim.h"
#include "udf.h"
UDF_PROTOTYPE( usrEmissivityExample ) ;  /* function prototype */
Void usrEmissivityExample (
    UdfHd    udfHd,                      /* Opaque handle for accessing data */
	Real*    outVec,                     /* Output vector */
	Integer  nItems,                     /* Number of elements */
	Integer  vecDim                      /* = 1 */
) {
    Integer  elem ;                      /* an element counter */
    Real     temp0 ;                     /* lower temp. limit of band */
    Real     temp1 ;                     /* upper temp. limit of band */
    Real     eDef ;                      /* default emissivity */
    Real     eBand ;                     /* emissivity in temperature band */
    Real*    temp ;                      /* temperature */
    Real*    usrVals ;                   /* user values */
udfCheckNumUsrVals( udfHd, 4 ) ;         /* check for error */
    usrVals  = udfGetUsrVals( udfHd ) ;  /* get the user vals */
    temp0    = usrVals[0] ;              /* lower temp  */
    temp1    = usrVals[1] ;              /* upper temp */
    eDef     = usrVals[2] ;              /* default emissivity */
    eBand    = usrVals[3] ;              /* band emissivity */
temp            = udfGetRsfData( udfHd, UDF_RSF_TEMPERATURE ) ;  /* get the temp. */
for ( elem = 0 ; elem < nItems ; elem++ ) {
    if ( temp[elem] >= temp0 && temp[elem] <= temp1 ) {
       outVec[elem] = eBand ;
    } else {
       outVec[elem] = eDef ;
    }
}
} /* end of usrEmissivityExample() */

The dimension of the returned emissivity vector, outVec, is the number of elements.

The multiplier_function parameter may be used to uniformly scale the emissivity values. The value of this parameter refers to the user-given name of a MULTIPLIER_FUNCTION command in the input file. For example, a ramped emissivity may be specified by:

EMISSIVITY_MODEL( "ramped emissivity model" ) {
   type                = constant 
   emissivity          = 0.4 
   multiplier_function = "ramped" 
   }
   MULTIPLIER_FUNCTION( "ramped" ) {
   type               = piecewise_linear 
   curve_fit_values   = { 1, 0.1 ; 10, 1 }
   curve_fit_variable = time_step
}

The diffused fraction defines the proportion of reflected radiation intensity at a surface which is diffused, i.e., the reflection may also have a specular component. If the radiation intensity reflection coefficient at the surface is defined by(2)

ρ = ρ^{S} + ρ^{D} = 1 - ε

then the diffused reflection coefficient,

ρ^{D}

, is defined in terms of the diffused fraction (

α

) and the emissivity of the surface by(3)

ρ^{D} = α (1 - ε)

and the specular reflection coefficient by(4)

ρ^{S} = (1 - α) (1 - ε)

α = 1

, then the reflection at the surface is completely diffused. If

α = 0

then the reflection is specular. The outgoing radiation intensity,

I

, at the surface in terms of the above two reflection coefficients is given by(5)

I (r_{w}, Ω_{i}) = ε (r_{w}) I_{B} (r_{w}) + \frac{ρ^{D} (r_{w})}{π} \sum_{n \cdot Ω_{j} < 0}^{N} ω_{j} I (r_{w}, Ω_{j}) | n \cdot Ω_{j} | + ρ^{S} (r_{w}) I (r_{w}, Ω_{S}) n \cdot Ω_{i} > 0

Michael Modest, Radiative Heat Transfer, Third Edition (2013)

where the first terms represent emission from the surface, the second term the diffused component incoming radiation heat flux and the third the specular component. The diffused component represents a sum over all radiation intensities along ordinates that are incident to the surface (i.e. a hemisphere of incoming radiation to the surface);

n

is the normal into the domain and

Ω_{j}

the jth ordinate direction. The ordinate direction (

Ω

), the total number of ordinate directions (

N

) and the weights (

ω

) are automatically defined by the order of the radiation_quadrature (S2, S4, S6, S8 & S10). The specular ordinate direction (

Ω_{S}

) is the direction that the radiation intensity must strike the surface to reflect in a specular fashion along the outgoing ordinate direction,

Ω_{i}

, and is given by(6)

Ω_{S} = Ω_{i} - 2 (Ω_{i} \cdot n) n

which means the angle that incident radiation intensity strikes the surface equals the angle of reflection.

To enable specular reflection a RADIATION_SURFACE must be defined and the diffused fraction, $α$ , and emissivity, $ε$ , must both be less than one.

For example,

RADIATION_SURFACE( "wall" ) {
	…
	emissivity_model = "wall_emissivity" ;
	diffused_fraction = 0.9 ;
}

with a typical emissivity model:

EMISSIVITY_MODEL( "wall_emissivity" ) {
	type = constant ;
	emissivity = 0.8 ;
}