Tied Interface (TYPE2)

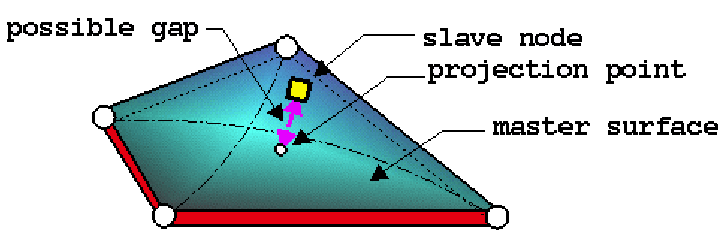
With a tied interface it is possible to connect rigidly a set of slave nodes to a master surface.

A tied interface (TYPE2) can be used to connect a fine mesh of Lagrangian elements to a coarse mesh or two different kinds of meshes (for example, spring to shell contacts).

A master and a slave surface are defined in the interface input cards. The contact between the two surfaces is tied. No sliding or movement of the slave nodes is allowed on the master surface. There are no voids present either.

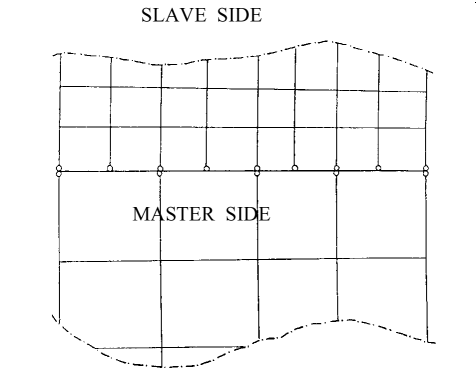
It is recommended that the master surface has a coarser mesh.

Accelerations and velocities of the master nodes are computed with forces and masses added from the slave nodes.

Kinematic constraint is applied on all slave nodes. They remain at the same position on their master segments.

Tied interfaces are useful in rivet modeling, where they are used to connect springs to a shell or solid mesh.

Spotweld Formulation

The slave node is rigidly connected to the master surface. Two formulations are available to describe this connection:

Default formulation
Optimized formulation

Default Spotweld Formulation

When Spot_flag=0, the spotweld formulation is a default formulation:

Based on element shape functions
Generating hourglass with under integrated elements
Providing a connection stiffness function of slave node localization
Recommended with full integrated shells (master)
Recommended for connecting brick slave nodes to brick master segments (mesh transition without rotational freedom)

Forces and moments transfer from slave to master nodes is described in Figure 3:

The mass of the slave node is transferred to the master nodes using the position of the projection on the segment and linear interpolation functions:(1)

{\bar{m}}_{m a s t e r}^{i} = m_{m a s t e r}^{i} + m_{s l a v e} * Φ_{i} (p)

Where,

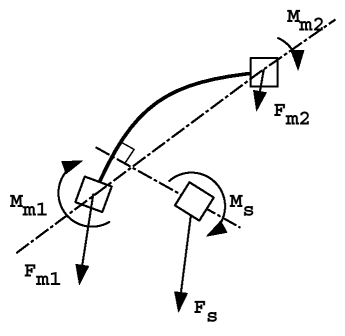
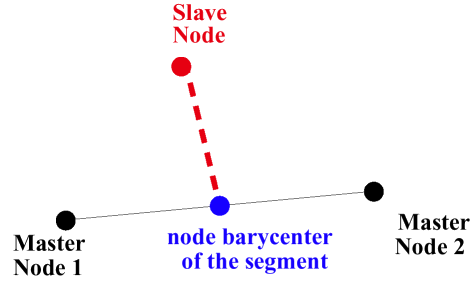
$p$: Denotes the position of the slave point
$Φ$: Weight function obtained by the interpolation equations

The inertia of the slave node is also transferred to the master nodes by taking into account the distance

d

between the slave node and the mater surface:(2)

{\bar{I}}_{m a s t e r}^{i} = I_{m a s t e r}^{i} + (I_{s l a v e} + m_{s l a v e} * d^{2}) * Φ_{i} (p)

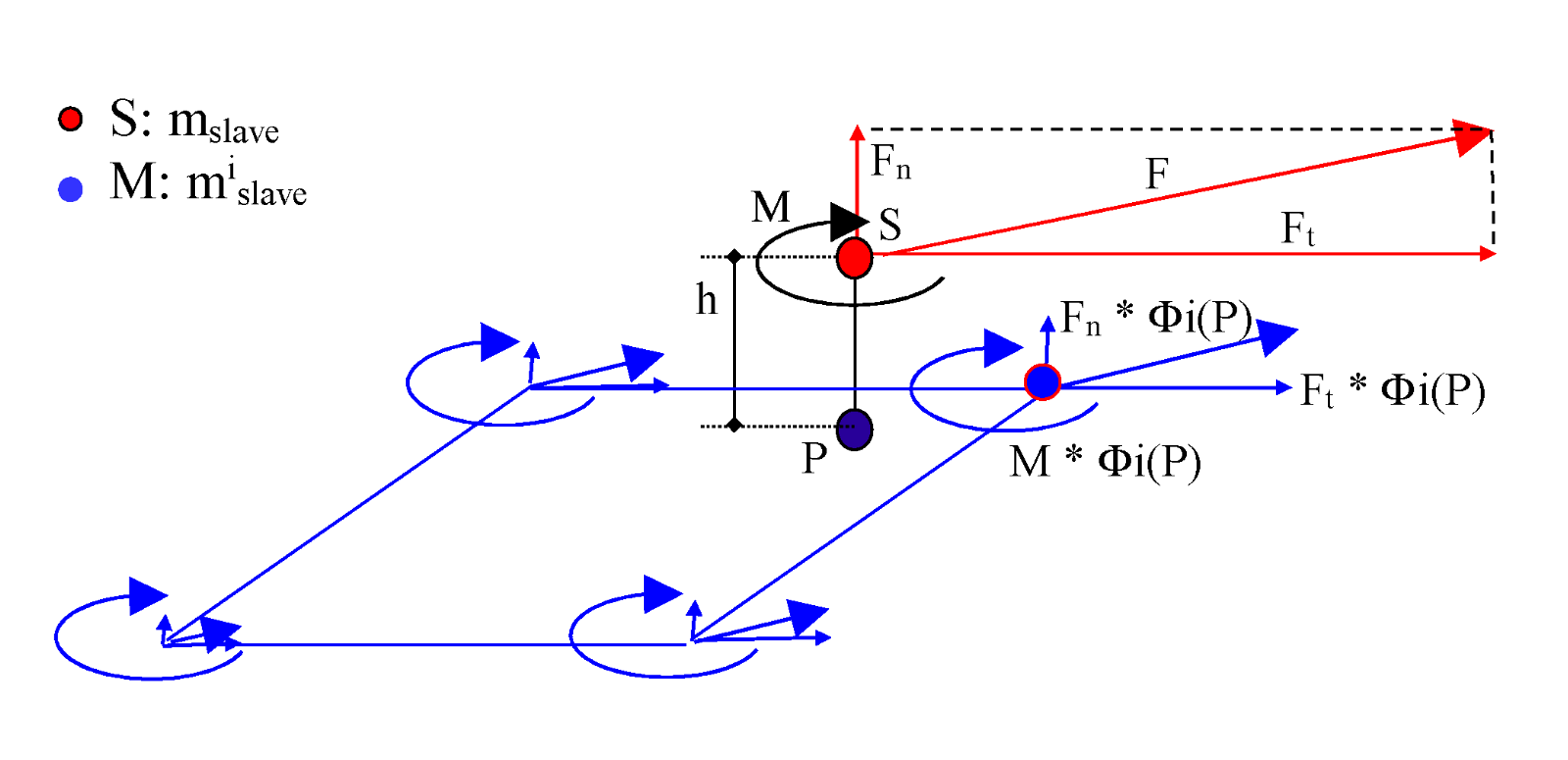
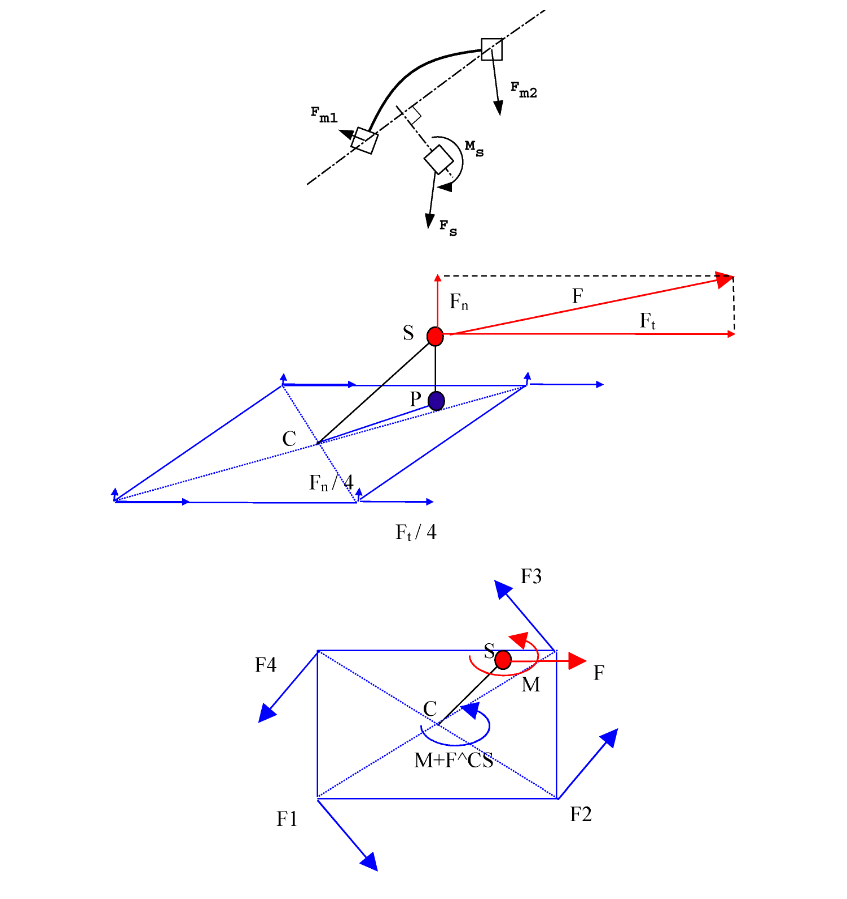
The term $m_{s l a v e} * d^{2}$ may increase the total inertia of the model especially when the slave node is far from the master surface.

The stability conditions are written on the master nodes:(3)

\begin{array}{l} {\bar{K}}_{m a s t e r}^{} = K_{m a s t e r}^{} + K_{s l a v e} * Φ_{i} (p) \\ {\bar{K}}_{m a s t e r}^{r o t a t i o n} = K_{m a s t e r}^{r o t a t i o n} + (K_{s l a v e}^{r o t a t i o n} + K_{s l a v e} * d^{2}) * Φ_{i} (p) \end{array}

The dynamic equilibrium of each master node is then studied and the nodal accelerations are computed. Then the velocities at master nodes can be obtained and updated to compute the velocity of the projected point

P

by:(4)

\begin{array}{l} V_{P}^{t r a n s l a t i o n} = \sum_{i} V_{m a s t e r i}^{t r a n s l a t i o n} Φ_{i} (p) \\ V_{P}^{r o t a t i o n} = \sum_{i} V_{m a s t e r i}^{r o t a t i o n} Φ_{i} (p) \end{array}

The velocity of the slave node is then obtained:(5)

\begin{array}{l} V_{s l a v e}^{t r a n s l a t i o n} = V_{P}^{t r a n s l a t i o n} + V_{P}^{r o t a t i o n} \otimes \vec{P S} \\ V_{s l a v e}^{r o t a t i o n} = V_{P}^{r o t a t i o n} \end{array}

With this formulation, the added inertia may be very large especially when the slave node is far from the mean plan of the master element.

Optimized Spotweld Formulation

When Spot_flag=1, the spotweld formulation is an optimized formulation:

Based on element mean rigid motion (i.e. without exciting deformation modes)
Having no hourglass problem
Having constant connection stiffness
Recommended with under integrated shells (master)
Recommended for connecting beam, spring and shell slave nodes to brick master segments

This spotweld formulation is optimized for spotwelds or rivets.

The slave node is joined to the master segment barycenter as shown in Figure 5.

Forces and moments transfer from slave to master nodes is described in Figure 6. The force applied at the slave node

S

is redistributed uniformly to the master nodes. In this way, only translational mode is excited. The moment

M + C S \otimes F

is redistributed to the master nodes by four forces

F_{i}

such that:(6)

F_{i} \propto \vec{A} \otimes C M_{i}

\sum_{i} C M_{i} \otimes F_{i} = M + C S \otimes F

Where,

$\vec{A}$: Normal vector to the segment

In this formulation the mass of the slave node is equally distributed to the master nodes. In conformity with effort transmission, the spherical inertia is computed with respect to the center of the master element

C

:(7)

I_{C}^{S l a v e} = I^{S l a v e} + m^{S l a v e} . d^{2}

Where,

d

is distance from the slave node to the center of element. In order to insure the stability condition without reduction in the time step, the inertia of the slave node is transferred to the master nodes by an equivalent nodal mass computed by:(8)

Δ m = \frac{I^{S l a v e} + m^{S l a v e} . d^{2}}{‖ \bar{I} ‖}, \begin{matrix}  \end{matrix} w i t h \begin{matrix}  \end{matrix} \bar{I} = \sum_{i = 1, ..4} (\begin{matrix} Y_{i}^{2} + Z_{i}^{2} & - X_{i} Y_{i} & - X_{i} Z_{i} \\ - X_{i} Y_{i} & X_{i}^{2} + Z_{i}^{2} & - Y_{i} Z_{i} \\ - X_{i} Z_{i} & - Y_{i} Z_{i} & X_{i}^{2} + Y_{i}^{2} \end{matrix})

Closest Master Segment Formulation

The master segment is found via 2 formulations:

Old formulation
New improved formulation

Old Search of Closest Master Segment Formulation

When I_search= 1, the search of closest master segment was based on the old formulation.

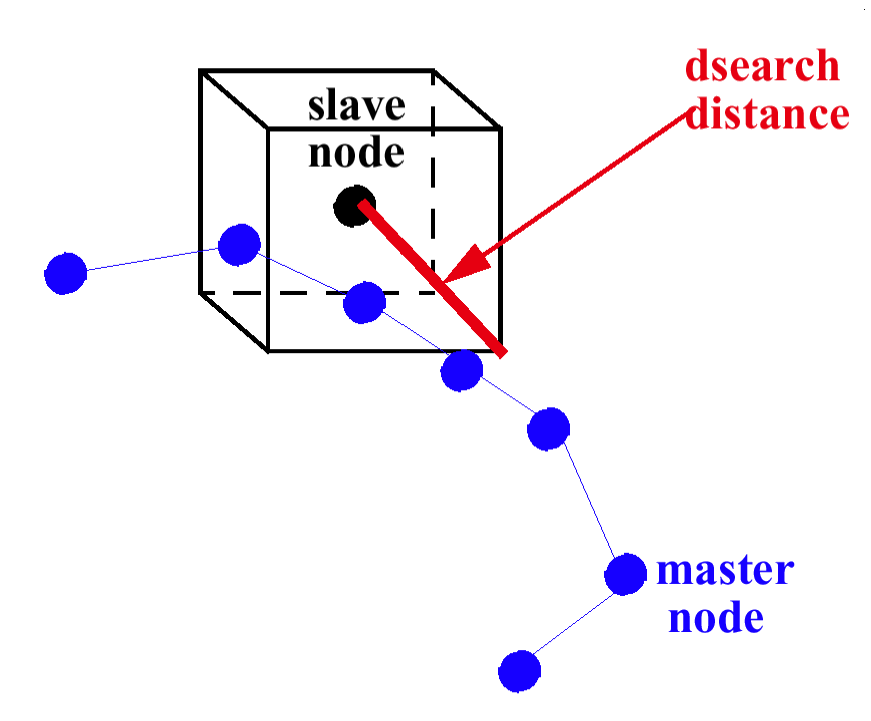
A box with a side equal to dsearch (input) is built to search the master node contained within this box.

The distance between each master node in the box and the slave node is computed.

The master node giving the minimum distance (dmin) is retained.

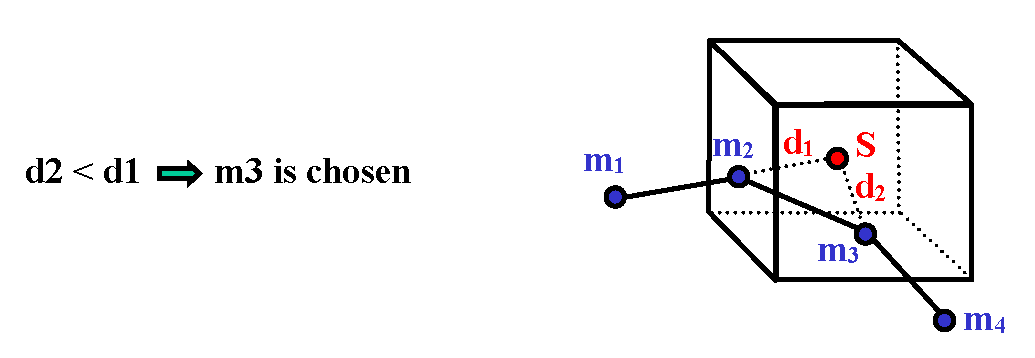
The segment is chosen with the selected node, (if the selected node belongs to 2 segments, one is selected at random).

New Improved Search of Closest Master Segment Formulation

When I_search=2, the search of closest master segment is based on the new improved formulation; a box including the master surface is built.

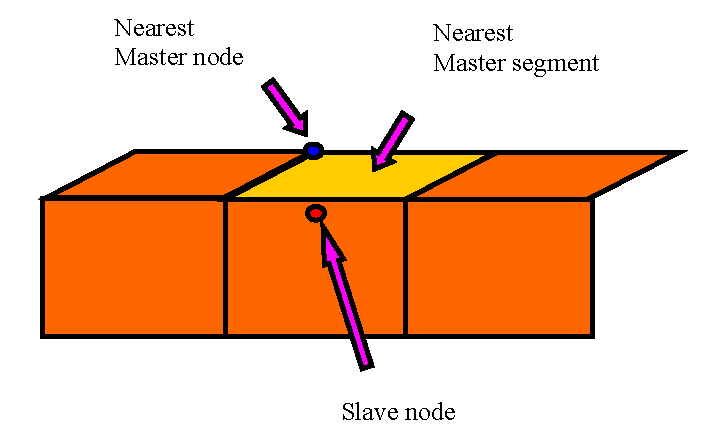
The dichotomy principle is applied to this box as long as the box contains only one master node and as long as the box side is equal to dsearch.

There are two solutions to compute the minimum distance, dmin:

The slave node is an internal node for the master segment, as shown in Figure 10.
The slave node is projected orthogonally on the master segment to give a distance that may be compared with other distances. Select the minimum distance:
Figure 10. Orthogonal Projection on the Master Segment

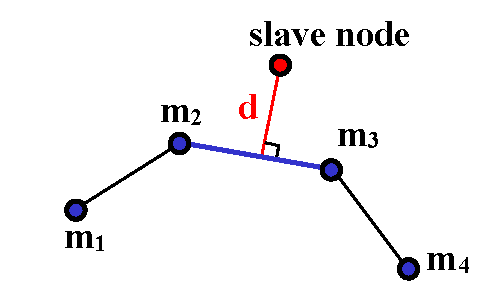
The segment that provides the minimum distance is chosen for the following computation.
The slave node is a node external to the master segment, as shown in Figure 11.
The distance selected is that between the slave node and the nearest master node.

Figure 11. Nearest Master Node

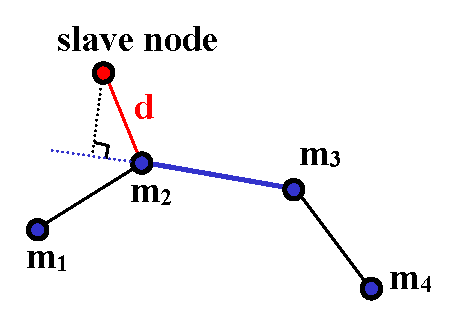
The segment is chosen using the selected node, (if the selected node belongs to 2 segments, one is chosen at random).