SPH Cells Distribution
The particles should be distributed through a hexagonal compact or a cubic net.
Hexagonal Compact Net
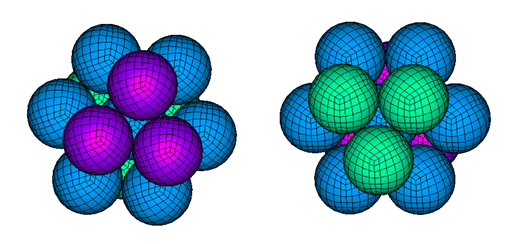
Figure 1. Local Views of the Hexagonal Compact Net
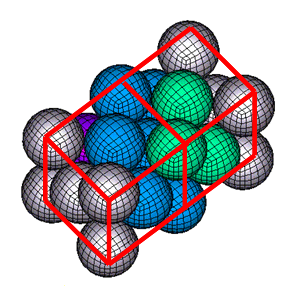
Figure 2. Perspective View of the Cubic Centered Faces Net
The nominal value h0 of h for the hexagonal compact net is the distance between any particle and its closest neighbor.
The mass of the particle which will be considered is the mass mp defined in the property which is associated to the part that the particle belongs to.
Notice that choosing h0 for the smoothing length insures naturally consistency up to order one, if the previous equation is satisfied.
| Distance d | Number of particles at distance d | Number of particles within distance d |
|---|---|---|
| h0 | 12 | 12 |
| 6 | 18 | |
| 24 | 42 | |
| 2h0 | 12 | 54 |
| 24 | 78 |
If SPH correction is used, notice that a small value for the smoothing length will increase the instability of the SPH method in case of tension behavior.
So, if using a hexagonal compact net and SPH corrections, it is recommended to set the smoothing length lower than the inter-particles minimum distance, only when there is no tension in the physical problem.
In the case of tension behavior, the value of the smoothing length can be set somewhat larger than the inter-particles distance, in order to limit the tension instability of SPH method. But a large value will result in excessive computational time.
Cubic Net
Let, c the side length of each elementary cube into the net.
| Distance d | Number of particles at distance d | Number of particles within distance d |
|---|---|---|
| c | 6 | 6 |
| 12 | 18 | |
| 8 | 26 | |
| 2c | 6 | 32 |
| 24 | 56 | |
| 24 | 80 | |
| 12 | 92 | |
| 3c | 6 | 98 |
From experience, a larger number of neighbors should be taken into account than in the hexagonal compact net, in order to solve the tension instability. A value of the smoothing length between 1.25c and 1.5c seems to be well-suited.
If choosing the smoothing length h=1.5c, each particle has 98 neighbors within the distance 2h.