Sprague-Geers Metric for Data Similarity
This section defines and provides examples of the Sprague-Geers Metric for Data Similarity.
Definition
- Calculate the metric M for magnitude difference and P for phase difference
as follows:
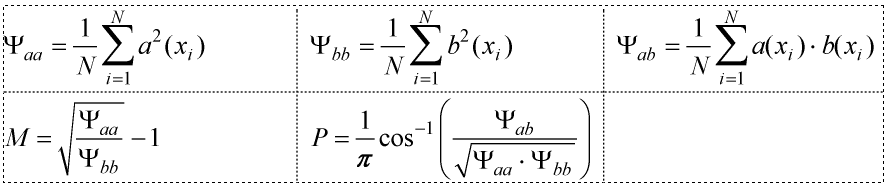
- Calculate the combined metric C as follows:C=1 is a perfect match. Metric C is what we want to show.Note: is known as the Sprague-Geers Combined Metric.
Example 1: Signals with the same overall magnitude, but drastically different slopes
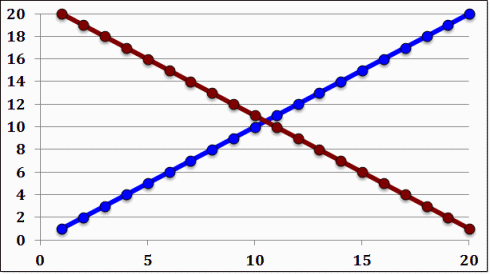
Figure 1.
Ψaa=143.50, Ψbb=143.50, Ψab=77.00, M+0.00, P=0.319714, C=0.680286
Example 2: Two very similar signals displaced in the y direction by 5%
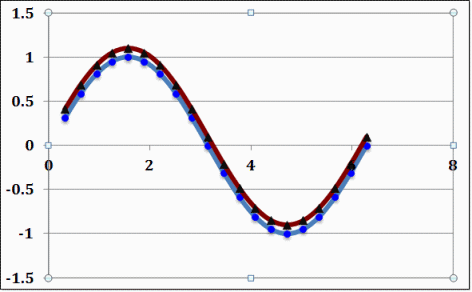
Figure 2.
Ψaa=0.50, Ψbb=0.51, Ψab=0.50, M=0.009852, P=0.044719, C=0.954208
Example 3: A synthesized MIT example for Dynamic Stiffness
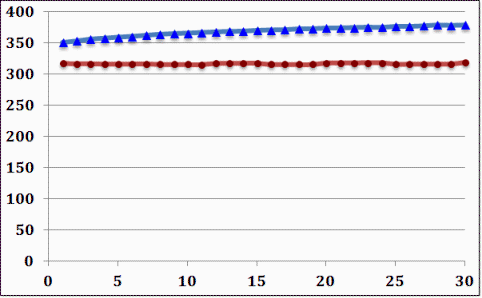
Figure 3.
Ψaa=3.39E+5, Ψbb=3.77E+5, Ψab=3.57E+5, M=0.051164, P=0.026831, C=0.942227
Example 4: A synthesized MIT example for Loss Angle
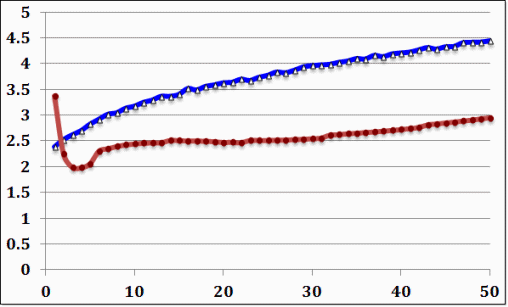
Figure 4.
Ψaa=1.39628E+1, Ψbb=6.67958, Ψab=9.59216, M=0.445811, P=0.037025, C=0.552654