ACU-T: 5200 Rigid-Body Dynamics of a Check Valve
This tutorial provides the instructions for setting up, solving and viewing results for a simulation of the opening of a pressure check valve. In this simulation, AcuSolve is used to compute the forces on the valve due to the time-varying inlet flow field and to compute the motion of the valve that results from these flow forces. This tutorial is designed to introduce you to a number of modeling concepts necessary to perform simulations of rigid-body dynamics.
- Transient simulation
- Use of a multiplier function to scale inlet boundary condition values
- Mesh motion
- Fluid-structure interaction with a rigid body
- Post-processing with AcuProbe
- Results animation
Prerequisites
You should have already run through the introductory tutorial, ACU-T: 2000 Turbulent Flow in a Mixing Elbow. It is assumed that you have some familiarity with AcuConsole, AcuSolve, and AcuFieldView. You will also need access to a licensed version of AcuSolve.
Prior to running through this tutorial, copy AcuConsole_tutorial_inputs.zip from <AcuSolve_installation_directory>\model_files\tutorials\AcuSolve to a local directory. Extract pressureCheckValve.x_t from AcuConsole_tutorial_inputs.zip.
Analyze the Problem
An important first step in any CFD simulation is to examine the engineering problem to be analyzed and determine the settings that need to be provided to AcuSolve. Settings can be based on geometrical components (such as volumes, inlets, outlets, or walls) and on flow conditions (such as fluid properties, velocity, or whether the flow should be modeled as turbulent or as laminar).
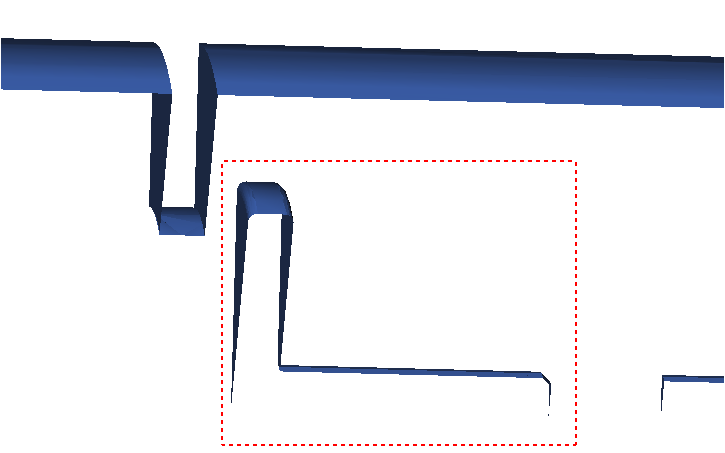
The problem to be addressed in this tutorial is shown schematically in Figure 1. It consists of a cylindrical pipe containing water that flows past a check valve with a shutter attached to a virtual spring (not included in the geometry). The inlet pressure varies over time and the movement of the shutter will be determined as a function of the balance of the fluid forces against the reactive force of the spring. The problem is rotationally periodic at 30° increments about the longitudinal axis, and it is assumed that the resulting flow is also rotationally periodic, allowing for modeling with the use of a wedge-shaped section. For this tutorial, a 30° section of the geometry is modeled, as shown in the figure. Modeling a portion of an rotationally periodic geometry leads to reduced computation time while still providing an accurate solution.

Figure 1. Schematic of Check Valve with Spring-Loaded Shutter
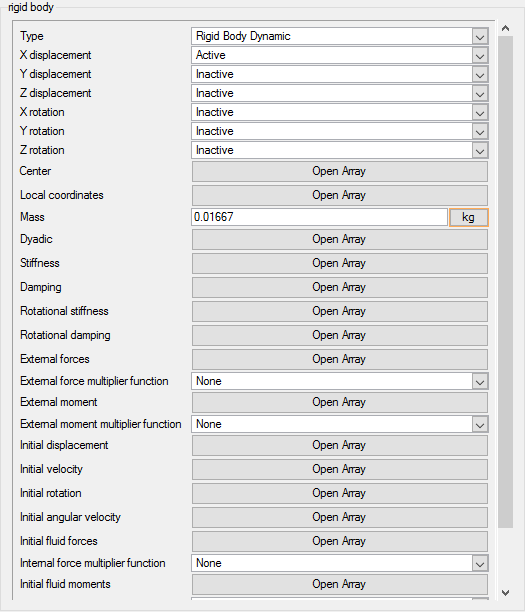
The pipe has an inlet diameter of 0.08 m, and is 0.4 m long. The check-valve assembly is 0.085 m downstream of the inlet. It consists of a plate 0.005 m thick with a centered orifice 0.044 m in diameter and a shutter with an initial position 0.005 m from the opening, simulating a nearly closed condition. The shutter plate is 0.05 m in diameter and 0.005 m thick. The shutter plate is attached to a stem 0.03 m long and 0.01 m in diameter. The mass of the shutter and stem is 0.2 kg and its motion is affected by a virtual spring with a stiffness of 2162 N/m. The motion of the valve shutter is limited by a stop mounted on a perforated plate downstream of the shutter.
Note that AcuSolve's internal rigid-body-dynamics solver is not able to simulate contact. Therefore, this problem is formulated to avoid contact between the valve and the stop.

Figure 2.
- Scale up the fluid forces calculated by AcuSolve by a factor
of 12 to represent the full load on the device when the displacement of the body is
computed.
Using this approach, the full stiffness of the valve spring is used in the rigid-body solution, and the full mass of the valve is used.
- Scale down the mass of the valve and the stiffness of the spring to by a factor of 12 to
match the fraction of the valve geometry to be modeled.
Using this approach, the loading passed to the rigid-body solver is not scaled.
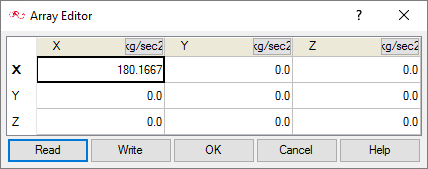
This second approach is used in this tutorial; the scaled mass of 0.0167 kg and the scaled stiffness of 180.1667 N/m will be used .

Figure 3.
The fluid in this problem is water, which has a density (ρ) of 1000 kg/m3 and a molecular viscosity (μ) of 1 X 10-3 kg/m-sec, as shown in the worksheet.

Figure 4.
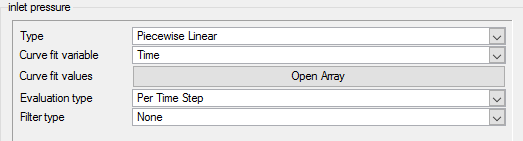
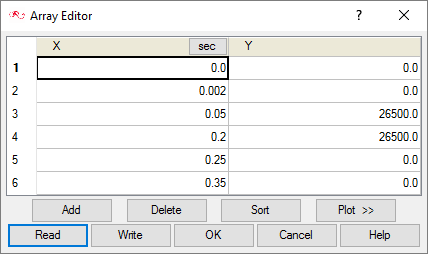
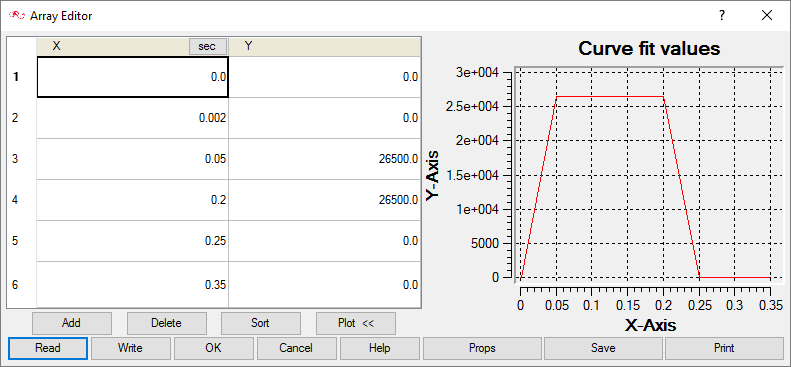
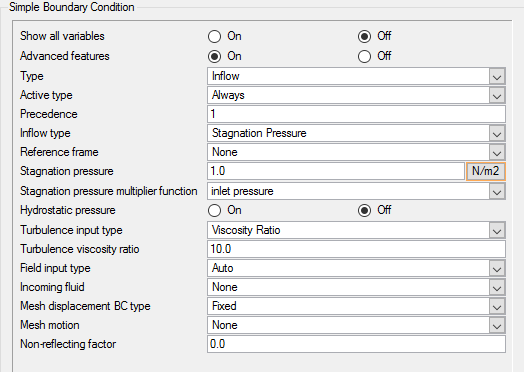
At the start of the simulation the flow field is stationary. Flow is driven by the pressure at the inlet, which varies over time as a piecewise linear function shown in Figure 5. As the pressure at the inlet rises, the flow will accelerate as the valve opens. The turbulence viscosity ratio is assumed to be 10.
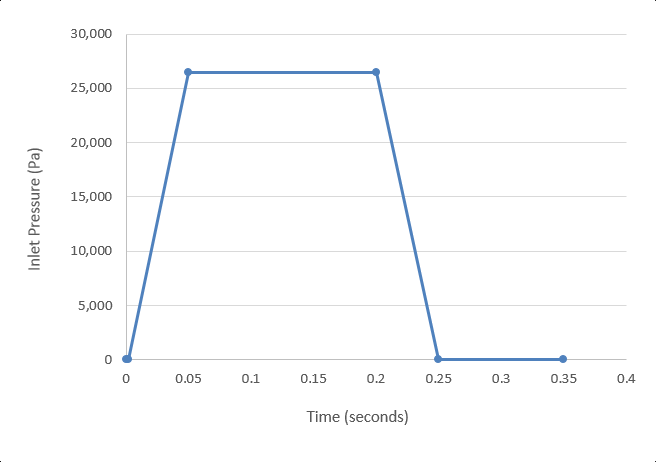
Figure 5. Transient Pressure at the Inlet
Prior simulations of this geometry indicate that the average velocity at the inlet reaches a maximum of 0.9 m/s. At this velocity, the Reynolds number for the flow is 72,000. When the Reynolds number is above 4,000, it is generally accepted that flow should be modeled as turbulent.

Figure 6.
Note that the initial conditions of the flow are actually laminar, however, the increase in flow velocity and flow around the valve shutter is expected to cause a rapid transition to turbulent conditions. Therefore, the simulation will be set up to model transient, turbulent flow. When performing a transient analysis, convergence is achieved at every time step based on the defined stagger criteria. Mesh motion will be modeled using arbitrary mesh movement (arbitrary Lagrangian-Eulerian mesh motion).

Figure 7.

Figure 8.
Another critical decision in a transient simulation is choosing the time increment. The time increment is the change in time during a given time step of the simulation. It is important to choose a time increment that is short enough to capture the changes in flow properties of interest, but does not require unnecessary computation time.
There are two methods commonly used for determining an appropriate time increment. The first method involves identification of the time scales of the transient behaviors of interest and setting the time increment to sufficiently resolve those behaviors. The second method involves setting a limit on the number of mesh elements that the flow can cross in a given time step. A convenient metric for the number of mesh elements crossed per time step is the Courant-Friederichs-Lewy number, or CFL number. With this method, the time increment can be computed from the mesh size, the flow velocity, and the desired CFL number.

Figure 9.

Figure 10.
AcuSolve allows for mesh refinements in a user-defined region that is independent of geometric components of the problem such as volumes, model surfaces, or edges. It is useful to refine the mesh in areas where gradients in pressure, velocity, eddy viscosity, and the like are steep.

Figure 11.
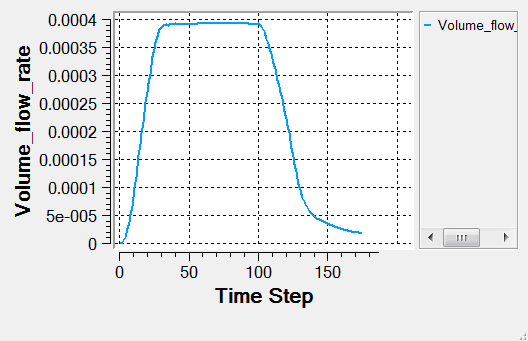
Once a solution is calculated, the flow properties of interest are the displacement of the moving surface, the mass flow rate at the outlet, pressure contours on the symmetry plane, and velocity vectors on the symmetry plane.
Define the Simulation Parameters
Start AcuConsole and Create the Simulation Database
In this tutorial, you will begin by creating a database, populating the geometry-independent settings, loading the geometry, creating groups, setting group attributes, adding geometry components to groups, creating a multiplier function, and assigning mesh controls and boundary conditions to the groups. Next you will generate a mesh and run AcuSolve to simulate the transient behavior. You will use AcuProbe to post-process mesh displacement and mass flow. Finally, you will visualize the results using AcuFieldView.
In the next steps you will start AcuConsole, create the database for storage of AcuConsole settings, and set the location for saving mesh and solution information for AcuSolve.
Set General Simulation Attributes
In the next steps you will set attributes that apply globally to the simulation. To simplify this task, you will use the BAS filter in the Data Tree Manager. The BAS filter limits the options in the Data Tree to show only the basic settings.
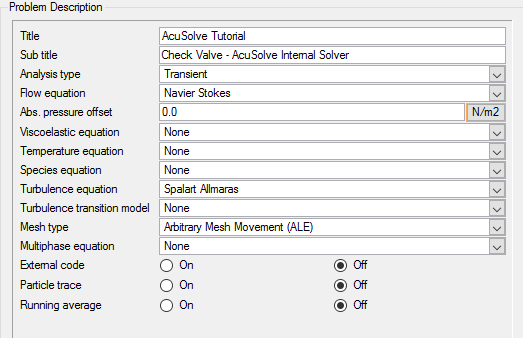
The general attributes that you will set for this tutorial are for turbulent flow, transient time analysis, and the use of arbitrary mesh movement.
Set Solution Strategy Attributes
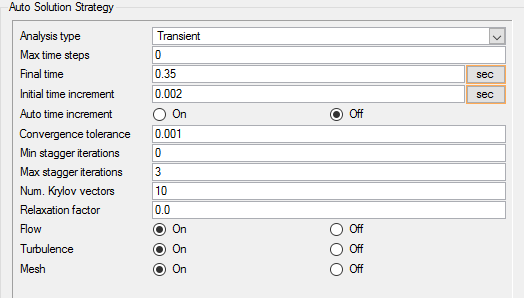
In the next steps you will set attributes that control the behavior of AcuSolve as it progresses during the transient solution.

Figure 15.
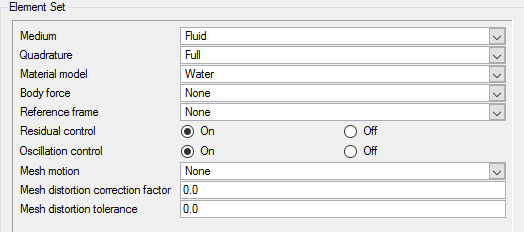
Set Material Model Attributes
AcuConsole has three pre-defined materials, Air, Aluminum, and Water.
In the next steps you will verify that the pre-defined material properties of water match the desired properties for this problem.

Figure 17.
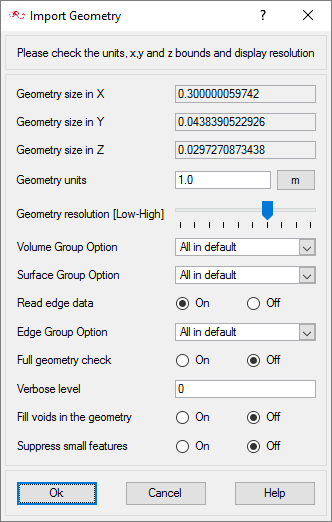
Import the Geometry and Define the Model
Import the Check Valve Geometry
Create Multiplier Function for Inlet Pressure
AcuSolve provides the ability to scale values as a function of time and/or time step during a simulation. This is achieved through the use of a multiplier function. In this tutorial, the inlet stagnation pressure varies as the simulation progresses. By taking advantage of multiplier functions, you can easily set up a function to model the pressure changes at the inlet.
In the next steps you will create a multiplier function for the pressure at the inlet. This multiplier function will be applied to the inlet later in this tutorial.

Figure 21.
To make the creation of the multiplier functions as simple as possible, you will use the PB* filter in the Data Tree Manager.
Create Mesh Motion
AcuSolve uses the mesh-motion settings to define the movement of nodes within the model. In this tutorial, you will use a special case of this command that solves the dynamic equations of motion to determine the motion of the nodes. This type of mesh motion is referred to as a rigid-body dynamic. In this simulation, you will specify two inputs to define the behavior of the rigid body; the mass of the valve shutter and the stiffness of the spring that resists the movement of the valve shutter.
- Create the mesh-motion definition (this set of steps).
- Assign the mesh-motion instance to a surface group.
- Revisit the mesh-motion settings to couple the forces on the surface with the displacement of the body.
In the next steps you will create a mesh motion of type rigid body to simulate the valve shutter and virtual spring. This mesh motion defines how the valve responds to the flow forces. To simplify this task, you will use the FSI filter in the Data Tree Manager. The FSI filter limits the options in the to show only the settings related to fluid-structure interactions.
Apply Volume Parameters
Volume groups are containers used for storing information about volumes. This information includes the list of geometric volumes associated with the container, as well as attributes such as material models and mesh sizing information.
When the geometry was imported into AcuConsole, all volumes were placed into the "default" volume container.
In the next steps you will rename the default volume group and set the material for the volume as water.
Create Surface Groups and Apply Surface Attributes
Surface groups are containers used for storing information about a surface. This information includes the list of geometric surfaces associated with the container, as well as attributes such as boundary conditions, surface outputs, and mesh sizing information.
In the next steps you will define surface groups, assign the appropriate attributes for each group in the problem, and add surfaces to the groups.
Set Inflow Boundary Conditions for the Inlet
In the next steps you will define a surface group for the inlet, assign the multiplier function to describe the transient pressure, and add the inlet from the geometry to the surface group.
Set Outflow Boundary Conditions for the Outlet
In the next steps you will define a surface group for the outlet, assign the appropriate attributes and add the outlet from the geometry to the surface group.
- Create a new surface group.
- Rename the surface to Outlet.
- Expand the Outlet surface in the tree.
- Double-click Simple Boundary Condition to open the detail panel.
- Change the Type to Outflow.
-
Add a geometry surface to the Outlet surface
container.
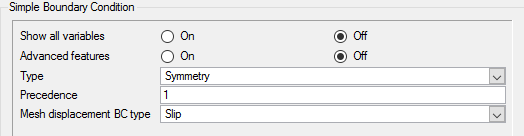
Set Symmetry Boundary Conditions for the Symmetry Planes
The problem is rotationally periodic, allowing for modeling with the use of a section. For this tutorial, a 30-degree section of the geometry is modeled. In order to take advantage of this, the front and rear faces of the section can be identified as symmetry planes, because the non-streamwise flow contribution is minimal. The symmetry boundary condition enforces constraints such that the flow field from one side of the plane is a mirror image of that on the other side.
In the next steps you will define a surface group for the symmetry plane on the front of the modeled section, and then create a second surface group for the back symmetry plane.
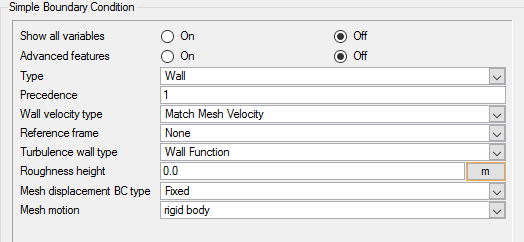
Set Wall Boundary Conditions for the Valve Shutter Walls
In the next steps you will define a surface group for the walls of the valve shutter, assign the appropriate settings, and add the faces from the geometry to the surface group. As part of the definition, you will assign the rigid-body mesh motion that you defined earlier to this surface.
Set Wall Boundary Conditions for the Pipe Walls
When the geometry was loaded into AcuConsole, all geometry surfaces were placed in the default surface group. In the previous steps, you selected geometry surfaces to be placed in the groups that you created. At this point, all that is left in the default surface group is the pipe wall. Rather than create a new container, add the wall surfaces in the geometry to it, and then delete the default surface container, you will rename the existing container.
Couple Mesh Motion to the Valve Wall
As the final step in enabling the use of mesh motion, you will revisit the mesh-motion definition to couple the mesh motion that you created earlier with the valve wall surface group. This step instructs AcuSolve to extract the forces on the valve from the set of surfaces that you specify in this step.
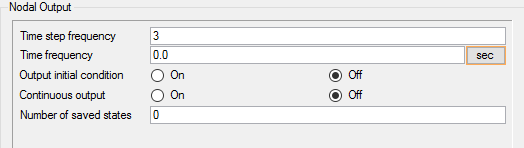
Set Nodal Output Frequency
In the next steps you will set an attribute that impacts how often results from the transient simulation are written to disk. Writing the results every three time steps produces a collection of output states that can be used to create an animation of the simulation once the run has completed. Note that more frequent output can be used, but it will result in higher disk space usage.
Assign Mesh Controls
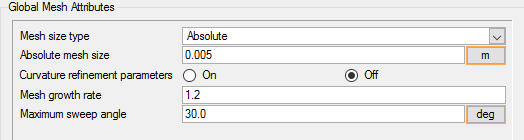
Set Global Meshing Parameters
Now that the simulation has been defined, attributes need to be added to define the mesh sizes that will be created by the mesher.
- Global mesh controls apply to the whole model without being tied to any geometric component of the model.
- Zone mesh controls apply to a defined region of the model, but are not associated with a particular geometric component.
- Geometric mesh controls are applied to a specific geometric component. These controls can be applied to volume groups, surface groups, or edge groups.
In the next steps you will set global meshing attributes. In subsequent steps you will create zone and surface meshing attributes.
Set Zone Meshing Parameters
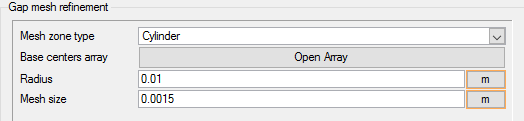
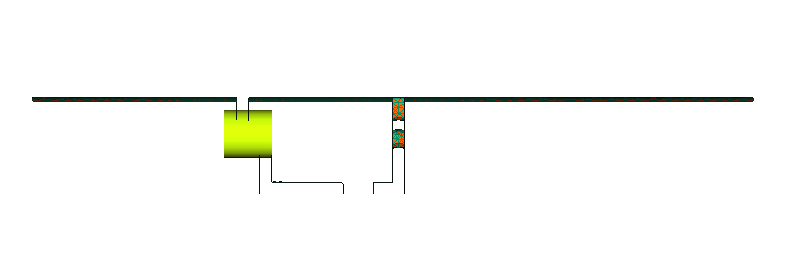
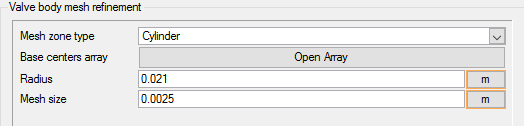
In addition to setting meshing characteristics for the whole problem, you can assign meshing attributes to a zone within the problem where you want to be able to resolve flow with a mesh that is more refined than the global mesh. A zone mesh refinement can be created using basic shapes to control the mesh size within that shape. These types of mesh refinement are used when refinement is needed in an area that does not correspond to a geometric item.
In the following steps you will add mesh refinements in the zone around the valve gap and around the valve body.
Set Zone Meshing Parameters for the Gap
In the next steps you will add a set of mesh attributes for a zone around the gap between the valve shutter and the orifice.
Set Zone Meshing Parameters for the Valve Body
In the next steps you will add a set of mesh attributes for a zone around the valve body.
Set Meshing Attributes for Surface Groups
In the following steps you will set meshing attributes that will allow for localized control of the mesh size on surface groups that you created earlier in this tutorial. Specifically, you will set local meshing attributes that control the growth of boundary layer elements normal to the surfaces of the pipe walls and valve walls.
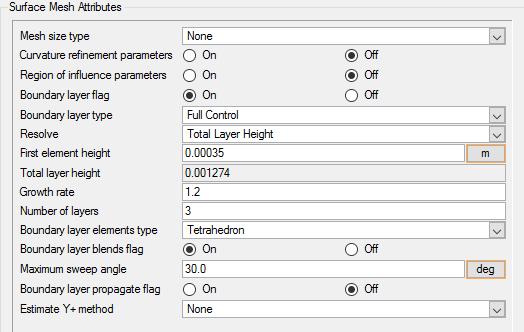
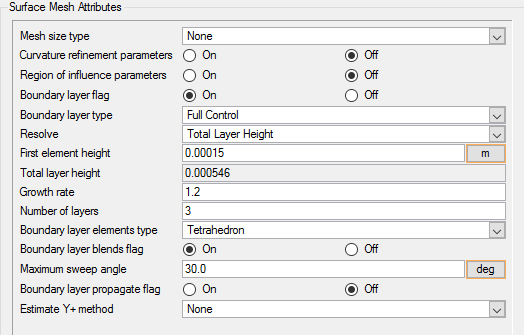
Set Surface Meshing Attributes for the Pipe Walls
In the next steps you will set meshing attributes that allow for localized control of the mesh near the walls of the pipe. The mesh size on the wall of the pipe will be inherited from the global mesh size that was defined earlier. The settings that follow will only control the growth of the boundary layer from the walls of the pipe into the fluid volume.
Set Surface Meshing Attributes for the Valve Walls
In the next steps you will set meshing attributes that allow for localized control of the mesh size near the walls of the valve shutter assembly.
Generate the Mesh
In the next steps you will generate the mesh that will be used when computing a solution for the problem.
Compute the Solution and Review the Results
Run AcuSolve
In the next steps you will launch AcuSolve to compute the solution for this case.
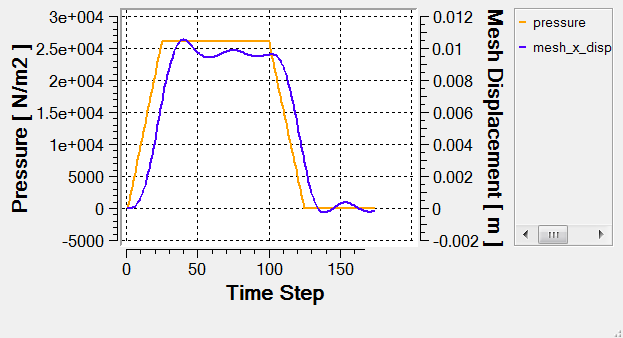
Monitor the Solution with AcuProbe
While AcuSolve is running, you can monitor the inlet pressure and displacement of the valve using AcuProbe.
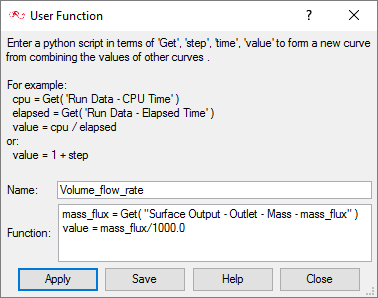
Post-Process Flow Rate with AcuProbe

In the next steps you will create a user function for the display of volume flow rate in AcuProbe.
View Results with AcuFieldView
Now that a solution has been calculated, you are ready to view the flow field using AcuFieldView. AcuFieldView is a third-party post-processing tool that is tightly integrated toAcuSolve. AcuFieldView can be started directly from AcuConsole, or it can be started from the Start menu, or from a command line. In this tutorial you will start AcuFieldView from AcuConsole after the solution is calculated by AcuSolve.
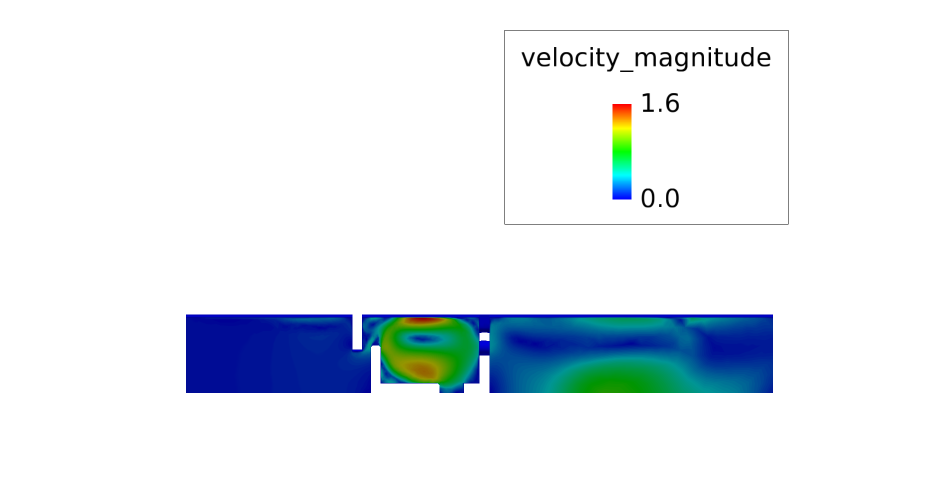
In the following steps you will start AcuFieldView, display velocity magnitude and animate the view to show mesh displacement. You will then display velocity vectors and pressure contours when the valve shutter is at maximum displacement.
Start AcuFieldView
Display Velocity Magnitude on the Front Symmetry Plane
In the next steps you will create a boundary surface to display contours of velocity magnitude on the front symmetry plane of the modeled slice.
These steps are provided with the assumption that you are able to manipulate the view in AcuFieldView to have a white background, perspective turned off, outlines turned off, and the viewing direction set to +Z. If you are unfamiliar with basic AcuFieldView operations, refer to Manipulate the Model View in AcuFieldView .
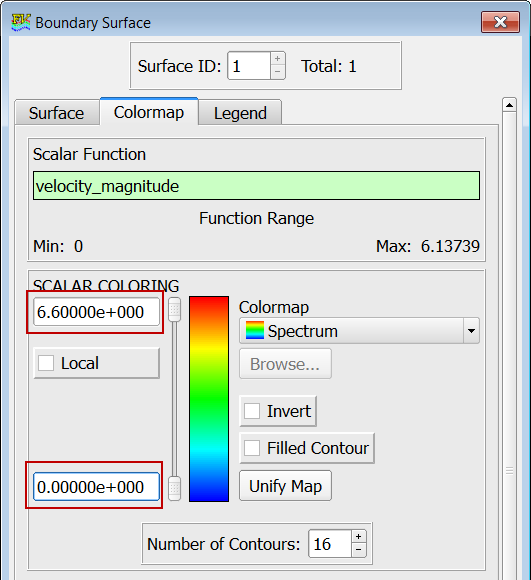
Animate the Display of Velocity Magnitude
In the next steps you will create a transient sweep and save it as an animation that can be viewed independently of AcuFieldView. As a first step, you will change the colormap used by the legend.
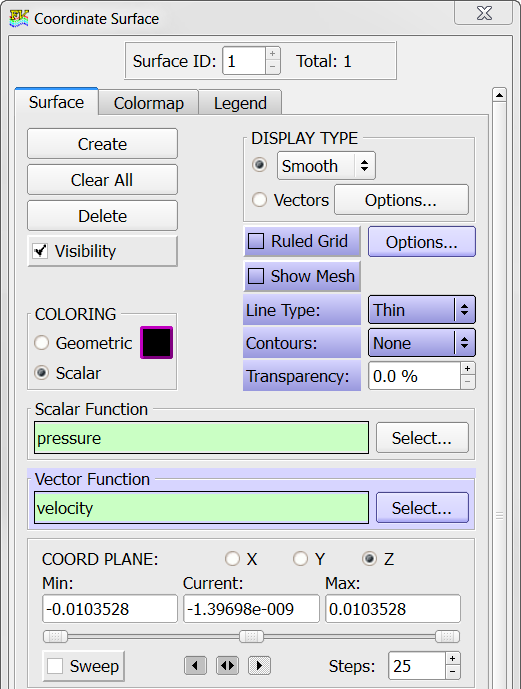
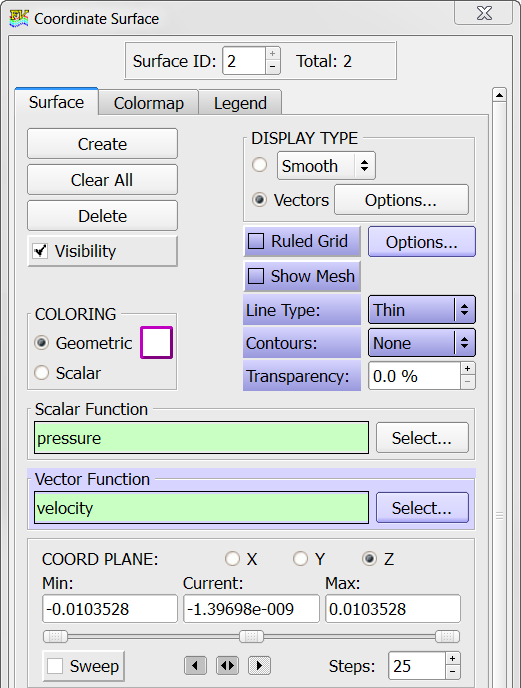
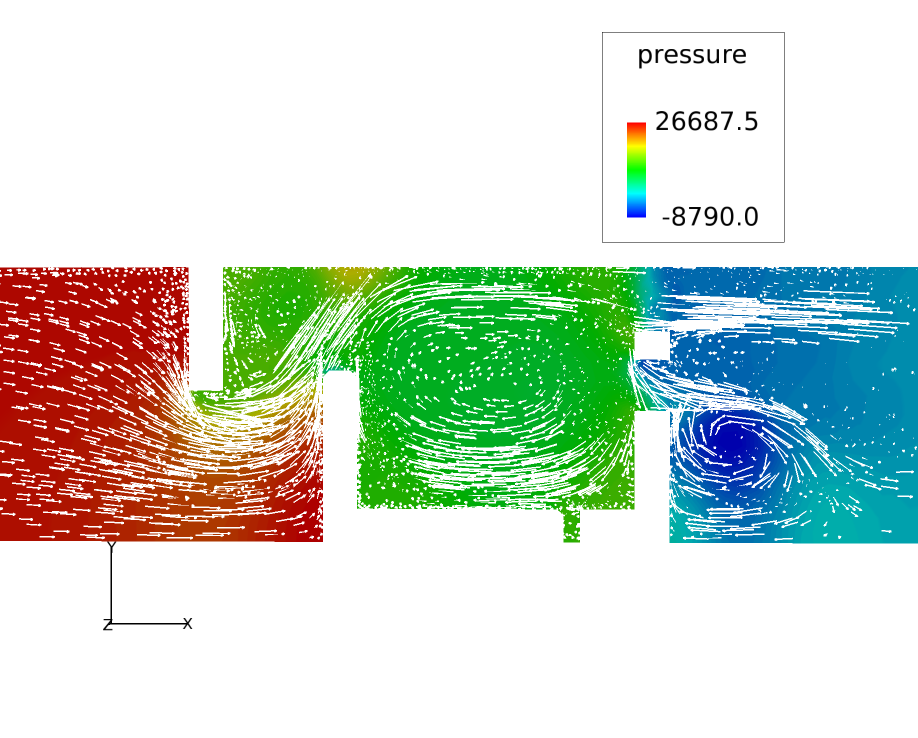
Display Pressure Contours and Velocity Vectors on a Mid-Z Coordinate Surface
In the next steps you will create a coordinate surface at the mid-Z plane of the modeled section. You will then display pressure contours and velocity vectors on that surface.